The scientific method gave rise to many world-changing discoveries. Galileo managed to mathematically describe the motion of falling objects and found evidence confirming Copernicus’s heliocentric model of the solar system, Harvey documented the circulation of blood, Van Leeuwenhoek discovered single-celled organisms, William Gilbert discovered that the Earth was a magnet, Torricelli studied air pressure and the vacuum, Boyle studied the properties of gases, Huygens studied waves and circular motion, but the greatest discovery was undoubtedly Newton’s discovery of the universal law of gravitation, the first mathematically precise theory of gravity.
Newton’s discovery relied heavily on the work of Kepler, who had discovered three mysterious laws of planetary motion. Despite having found these laws, Kepler was not able to explain them. Newton finally put all the pieces together. He showed how a single gravitational force could explain both the trajectory of falling objects on earth and all three of Kepler’s laws of planetary motion. He thereby conclusively disproved Aristotle’s notion that earth and heaven require two distinct sets of natural laws. As a result, it is often said that Newton unified terrestrial and celestial physics, making him arguably the greatest genius who has ever lived.
Copernicus
Just before his death in 1543, the Polish astronomer Nicolaus Copernicus (1473–1543) published his masterpiece called On the Revolutions of the Heavenly Orbs. In his book, Copernicus presented a radically new model of the solar system, the heliocentric model, in which he situated the sun, and not the earth, at the center of the universe.
Fig. 464 – Copernicus (c. 1580) (Torun Regional Museum, Poland)
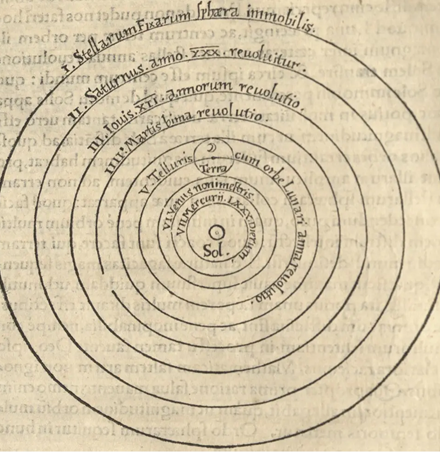
Fig. 465 – The heliocentric model according to Copernicus, from his On the Revolutions of the Heavenly Orbs.
Copernicus made his discovery by solving a problem that had been known since the time of the ancient Greeks. As seen from the earth, the planets seem to periodically stop, move back a little, stop again, and then move onwards on their trajectory (as is depicted in the chapter “Sacred Geometry” in Part I of the book). This backward motion is called retrograde motion. Copernicus showed that the apparent backward motion of the planets was not caused by the planets themselves, but rather by the fact that we are viewing these planets from yet another planet—namely, the earth—that is itself also moving around the sun. Through a calculation, he showed that as seen from the sun, the planets moved in simple circular orbits. With this reasoning, Copernicus finally fulfilled Plato’s wish to explain the motion of the planets in pure circular orbits.
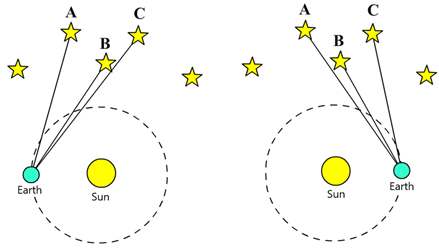
At the time, however, the world was not ready to accept his message. How could something as heavy as the earth be moving? Why don’t we notice this movement? And if the earth isn’t at the center of the universe, why don’t objects fall towards the sun instead of the earth? On top of these sensible questions, there also seemed to be hard evidence that the earth was standing still. In the heliocentric case, his opponents reasoned, the constellations should change shape over the year because we will be observing the stars from a different angle (see Fig. 466). We call this the parallax effect. Astronomers had tried to measure this effect but could not find it. To counter this criticism, Copernicus had to assume (without evidence) that the stars were so incredibly far away that the effect was too small to measure. This, however, required distances that far exceeded the then-accepted distance of the stars.
Fig. 466 – The parallax effect. On the left, star B and C appear close together. On the right, star A and B appear close together (S. P. Dinkgreve, worldhistorybook.com)
Although not many of his contemporaries were willing to accept his revolutionary new theory, some did agree that his model simplified calculations. Erasmus Reinhold (1511–1553) even used Copernicus’s model to improve Ptolemy’s prediction of planetary motion, yet even he made it clear that he did not believe in the model, but only used it as a useful mathematical tool.
The mechanical philosophy
But if the planets revolve around the sun, by what mechanism does this happen? An early attempt to solve this problem was proposed by Descartes in his work called The World. Descartes had been an early advocate of the mechanical philosophy, which proposes that the universe can be understood as a machine, like the inner workings of a clock. Similar to atomism, it was an attempt to radically reduce the complexity of the world through some simple mechanisms. In an attempt to understand how the sun could keep the planets in orbit without touching them, he imagined the solar system was filled with an undetectable substance called the ether. The ether rotated around the sun, creating a vortex that dragged the planets along in a circular orbit (Fig. 468). Descartes also famously applied the mechanistic approach to the human body (Fig. 467). In his Treatise on Man, we read:
I would like you to reflect […] on how all the functions that I have attributed to this machine, such as the digestion of food, the beating of the heart and arteries, the nutrition and growth of the members, respiration, waking and sleep, reception of light, sound, smell, taste, heat and such qualities by the external sense organs, the impression of these sensory ideas on the organ of common sense and imagination, and the retention or imprinting of these ideas in the memory, occur. […] These functions follow completely naturally in this machine solely from the disposition of the organs, no more nor less than those of a clock or other automaton from its counterweights and wheels. [285]
Fig. 467 – The functioning of the nerves by Descartes, from his Treatise on Man.
Hobbes
Thomas Hobbes (1588–1679), another early advocate of mechanical philosophy, did the same in his work Leviathan:
For what is the heart, but a spring; and the nerves, but so many strings; and the joints, but so many wheels, giving motion to the whole body, such as was intended by the artificer? [286]
While Descartes still believed in an immortal and immaterial soul, Hobbes gave a fully materialistic account of the human body. In his view there was no soul that survives death and therefore no afterlife. Similarly, his universe was entirely deterministic, and as a result also immoral and without purpose. Hobbes also did away with Aristotle’s notion that the purpose of reason was to understand the universe. Instead, he believed its main purpose was to simply figure out the best ways to fulfill our passions. Yet even Hobbes still believed in God, albeit a material God.
Fig. 468 – The ether model according to Descartes, from his Principia Philosophiae.
Analytic geometry
Rene Descartes also revolutionized mathematics by inventing the modern symbolic notation of algebra. When algebra came to Europe, equations were still written down in full sentences. This is doable for simple equations, but quickly becomes incomprehensible when equations become more complex. Robert Recorde (c. 1512–1558) helped solve this problem by developing the modern symbols for addition (“+”), subtraction (“–”), and equality (“=”). Francois Viète (1540–1603) took the next step by using letters to represent variables. In his masterpiece called La Geometrie, Descartes began to use x and y as variables and a, b, and c as constants. He also invented the use of superscripts for powers and developed the modern square root sign.
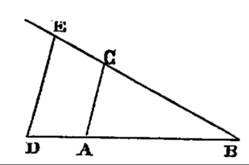
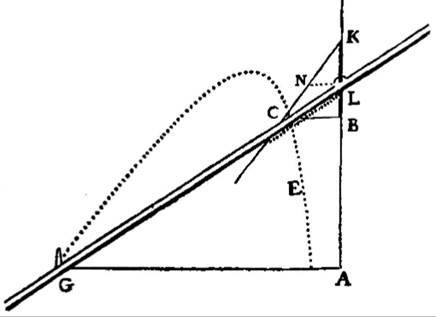
Even more important was Descartes’s invention of the Cartesian coordinate system (Cartesius is the Latinized name of Descartes). His invention ingeniously combined the geometry of the Greeks with the algebra of the Arabs, giving rise to what he called analytic geometry. Descartes started this exploration by constructing geometric devices that could be used to solve algebraic equations. Take, for instance, the instrument depicted in Fig. 469. By using the proportionality of the triangles ABC and DBE, he found that:
![]()
If we make length AB equal to “1”, this equation becomes:
![]()
This can be rewritten into:
![]()
Fig. 469 – Geometric devices to solve equations, from La Geometrie by Descartes (1673)
Fig. 470 – Another geometric device, from La Geometrie (1673)
From this equation, we have learned that by measuring length DE, we can find the answer to the multiplication of lengths BD and AC. Fig. 469 is, therefore, a machine with which we can “measure” the answer of any multiplication. He then went on to more complex examples, allowing him to measure, among other things, the square root of numbers and the solution to quadratic and cubic equations (see, for instance, Fig. 470).
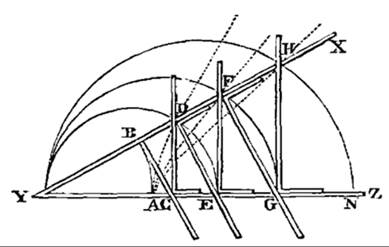
An even more revolutionary machine is depicted in Fig. 471. The figure shows a machine that is fixed at point G and can move up and down along line AK. When this motion is made, point C traces a curve that is depicted by the dotted line. Whereas his earlier geometric machines allowed him to find one solution for one setting, the dotted line describes an infinite set of solutions in one still image, which we today call a graph. Descartes then renamed the distance BC to x and AB to y, and he then used these distances as coordinates to describe the location of point C relative to point A. These line elements later turned into the familiar x- and y-axis.
Fig. 471 – A geometric device used to create a graph, from La Geometrie by Descartes (1673)
With his method, Descartes showed with pride that he could solve all the problems from ancient Greek mathematics, but in far fewer steps and without having to commit endless theorems to memory.
A few decades later, Newton would take La Geometrie to the next level with his invention of calculus.
Galileo
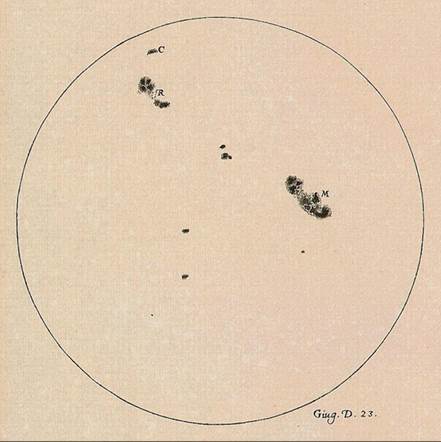
The great Italian physicist Galileo (1564–1642) was the first to use a telescope to study the heavenly bodies.[19] With this new instrument, he made a number of discoveries that further discredited Aristotle’s geocentric model of the universe. When pointing his telescope at the moon, he found that it was covered with mountains and valleys. This refuted the Aristotelian idea that the moon was a perfect globe made from a perfect heavenly fifth element. He then discovered that the sun wasn’t perfect either. It was covered with dark spots, called sunspots. Looking at these spots over several days, he discovered that they moved, suggesting that the sun rotates around its own axis. This made it more credible that the earth was doing the same thing. When looking at Venus, Galileo discovered it went through all its phases, just like the moon. He then showed this was only possible if Venus orbited the sun.
When looking at Jupiter, he was again surprised. It turned out that Jupiter had four moons. This was also inconsistent with the geocentric model, which assumed that all heavenly bodies circled the Earth. With these observations, combined with Copernicus’s explanation of the retrograde motion of the planets, Galileo conclusively proved the heliocentric model of the solar system.
Fig. 472 – A sketch of sunspots by Galileo, from History and Demonstrations Concerning Sunspots and their Properties (1613) The book contains over thirty drawings showing how the sunspots move over time, suggesting that the sun is rotating on its axis (Library of Congress)
Fig. 473: Jupiter and its four moons (Jan Sandberg, PD)
Experiment over authority
Galileo also understood that in science, the ability to confirm a claim experimentally should trump appeals to authority. This attitude, however, was not always shared by his contemporaries. When Galileo told his colleagues to look through his telescope to see Jupiter’s moons, they refused. So convinced were they by the authority of Aristotle, that they saw no need to confirm their beliefs with observation. In a letter to the astronomer Johannes Kepler, Galileo wrote:
My dear Kepler, what would you say of the learned here, who, replete with the pertinacity of the asp, have steadfastly refused to cast a glance through the telescope? What shall we make of this? Shall we laugh, or shall we cry? [287]
Fig. 474 – Galileo (1636) (National Maritime Museum, Britain)
In a letter to Christina de Lorraine (1565–1637), the duchess of Tuscany, Galileo even claimed he was unwilling to place the authority of scripture above demonstration in nature, for God is “excellently revealed in Nature’s actions.” We read:
I think that in discussions of physical problems we ought to begin not from the authority of scriptural passages but from sense experiences and necessary demonstrations. [...] Nature [...] is inexorable and immutable; she never transgresses the laws imposed upon her, or cares a whit whether her abstruse reasons and methods of operation are understandable to men. For that reason it appears that nothing physical which sense experience sets before our eyes, or which necessary demonstrations prove to us, ought to be called in question (much less condemned) upon the testimony of biblical passages which may have some different meaning beneath their words. For the Bible is not chained in every expression to conditions as strict as those which govern all physical effects; nor is God any less excellently revealed in Nature’s actions than in the sacred statements of the Bible. Perhaps this is what Tertullian meant by these words: “We conclude that God is known first through Nature, and then […] by doctrine. By Nature in His works and by doctrine in His revealed word.”
From this I do not mean to infer that we need not have an extraordinary esteem for the passages of holy Scripture. [...] I should judge that the authority of the Bible was designed to persuade men of those articles and propositions which, surpassing all human reasoning could not be made credible by science, or by any other means than through the very mouth of the Holy Spirit. [...] But I do not feel obliged to believe that that same God who has endowed us with senses, reason, and intellect has intended to forgo their use and by some other means to give us knowledge which we can attain by them. He would not require us to deny sense and reason in physical matters which are set before our eyes and minds by direct experience or necessary demonstrations. This must be especially true in those sciences of which but the faintest trace […] is found in the Bible. Of astronomy; for instance, so little is found that none of the planets except Venus are so much as mentioned, and this only once or twice under the name of “Lucifer.” [288]
The Leaning Tower of Pisa
Galileo also extensively studied falling bodies. We know from one of his students that Galileo dropped two balls with different masses from the Leaning Tower of Pisa. While Aristotle had assumed that a ball with twice the mass would reach the ground twice as fast, Galileo found that both objects reached the ground at about the same time. Galileo also predicted this outcome based on a thought experiment—an experiment not conducted in real life, but rather, logically played out in the mind. Writing in the form of a dialogue, he let his character Saviati explain:
Salviati: If then we take two bodies whose natural speeds are different, it is clear that on uniting the two, the more rapid one will be partly retarded by the slower, and the slower will be somewhat hastened by the swifter. Do you not agree with me in this opinion?
Simplicio: You are unquestionably right.
He then argued that a similar argument could be made that the two united masses are heavier as a whole and should, therefore, speed up instead of slow down. This is an internal contradiction in Aristotle’s theory. We read:
Thus you see how, from your assumption that the heavier body moves more rapidly than the lighter one, I infer that the heavier body moves more slowly. [289]
Because of the logical contradiction, Galileo concluded that Aristotle’s theory couldn’t possibly be right and that the only correct conclusion was to assume that the balls hit the floor at the same time (as long as air friction can be neglected).[20]
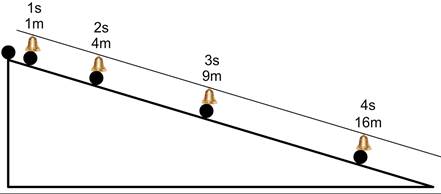
Galileo also discovered a mathematical law describing falling objects. He did so by moving balls down a smooth ramp. He found that after two seconds, the ball had moved four times as much as after the first second. After three seconds, it had moved nine times as much, and after four seconds, it had moved sixteen times as much (see Fig. 475). From this, he concluded that the distance traveled by a falling object was proportional to the square of the fall time.
Fig. 475 – Galileo’s experiment to study falling objects. Notice that the square of the fall time is proportional to the distance travelled. As Galileo had no stopwatch, he used bells to measure time. He placed the bells in such a way that they rang at a fixed interval (S. P. Dinkgreve, worldhistorybook.com)
Impressed by the mathematical character of this law of nature, he famously claimed that the Book of Nature must be written in the language of mathematics. In his own words:
Philosophy is written in this grand book—I mean the universe—which stands continually open to our gaze, but it cannot be understood unless one first learns to comprehend the language in which it is written. It is written in the language of mathematics, and its characters are triangles, circles, and other geometric figures, without which it is humanly impossible to understand a single word of it; without these, one is wandering about in a dark labyrinth. [290]
Galilean relativity
Galileo also expanded on the work of the medieval scientist Nicole Oresme. Oresme had claimed that objects behave the same at rest as they do on a platform moving with constant velocity. This is now often called the Galilean theory of relativity. Galileo confirmed this principle by dropping a rock from the mast of a uniformly moving ship. The rock hit the floor at the base of the mast, just as it did when the ship was at rest. Similarly, he found that people don’t jump further in one direction or another in a moving ship, nor does the smoke formed by incense go more to one side than another. We read:
Have the ship proceed with any speed you like, so long as the motion is uniform and not fluctuating this way and that. You will discover not the least change in all the effects named, nor could you tell from any of them whether the ship was moving or standing still. [291]
Fig. 476 – A modern depiction of Galileo’s thought-experiment (S. P. Dinkgreve, worldhistorybook.com)
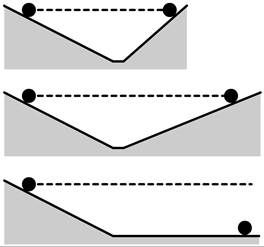
To further understand uniform motion, Galileo devised another thought experiment. He imagined a ball rolling down a frictionless hill and up another (see the top image of Fig. 476). Without friction, he claimed, the ball would reach the same height as it did at the starting point. He then imagined the right hill becoming less steep. For the ball to reach the same height, it now had to travel a greater distance (see the second image). Then he pushed the idea to the extreme. What if the angle of the right hill were made so small that it approaches zero degrees (see the third image)? In that case, the ball would travel an infinite distance to reach the same height. As a result, he concluded that objects continue in their motion indefinitely unless they are acted upon by an external force, such as friction. This was in contradiction with Aristotle’s idea that all matter on earth has the quality of wanting to be at rest.
He then went a step further. If a ball can move indefinitely, might this not explain how the earth indefinitely travels around the sun? And since the earth does not slow down over time, does this not imply that space is frictionless? From this, Galileo concluded that space must be a vacuum. This, too, contradicted Aristotle, who had claimed that a vacuum could not exist in nature (he had famously claimed: “nature abhors a vacuum”).
Galileo and the Church
Galileo’s defense of the heliocentric model, combined with his highly polemic writing style, got him into serious trouble with the Church. In 1615, the Church declared his theory heretical, banned his books, and forbade him from teaching on the subject. The Church, however, wasn’t completely unwilling. In 1632, the pope gave Galileo permission to publish a major work on the heliocentric system, called Dialogue Concerning the Two Chief World Systems, but under the condition that he would include the pope’s own view on the matter. Galileo added it in a short passage on the last page of his book, where it was vocalized by the foolish character Simplicio, after which the clever Salviati immediately refuted it. Understandably, this got him into trouble once more. We still have his sentence:
Whereas you, Galileo, son of the late Vincenzio Galilei, of Florence, aged seventy years, were denounced in 1615, to this Holy Office, for holding as true a false doctrine taught by many, namely, that the sun is immovable in the center of the world, and that the earth moves, and also with a diurnal motion; [and] also, [...] for answering the objections which were continually produced from the Holy Scriptures, by glozing the said Scriptures according to your own meaning. [...] Therefore (this Holy Tribunal being desirous to [avert] disorder and mischief which were [undermining] the Holy Faith) by the desire of his Holiness and the Most Eminent Lords, Cardinals of this supreme and universal Inquisition, the two propositions of the stability of the sun, and the motion of the earth, were qualified by the Theological Qualifiers as follows:
1. The proposition that the sun is in the center of the world and immovable from its place is absurd, philosophically false, and formally heretical; because it is expressly contrary to Holy Scriptures.
2. The proposition that the earth is not the center of the world, nor immovable, but that it moves, and also with a diurnal action, is also absurd, philosophically false, and, theologically considered, at least erroneous in faith.
Therefore [...], invoking the most holy name of our Lord Jesus Christ and of His Most Glorious Mother Mary, We pronounce this Our final sentence: We pronounce, judge, and declare, that you, the said Galileo [...] have rendered yourself vehemently suspected by this Holy Office of heresy [...] and in order that your grave and pernicious error and transgression may not remain altogether unpunished, and that you may be more cautious for the future, and an example to others, that they may abstain from similar delinquencies, we ordain that the book of the Dialogues of Galileo Galilei be prohibited by public edict.
We condemn you to the formal prison of this Holy Office during our pleasure, and by way of salutary penance, we enjoin that for three years to come, you repeat once a week the seven penitential Psalms. [292]
On the following day, the prison sentence was lowered to house arrest, which he remained under for the rest of his life.
In recent times, Galileo’s fight with the Church has often been portrayed as a fight between science and religion, yet Galileo too was a deeply religious man. It is more accurate to see it as a confrontation between a free-thinking maverick and a dogmatic religious institution.
Fig. 477 – Johannes Kepler by unknown painter (1610) (Kremsmunster Abbey, Germany)
Kepler
In 1576, the Danish astronomer Tycho Brahe (1546–1601) was granted an island by the king of Denmark on which he built an observatory-castle. From this castle, he conducted the most accurate observations of the motion of the planets up to that point, although still without a telescope. With his data, his student Johannes Kepler (1571–1630) made the next great step in our understanding of the solar system. He reconstructed the motion of the planets and discovered they moved in elliptical orbits, breaking with the ancient idea that heavenly orbs were “supposed” to move in perfect circles. This discovery became one of his three laws of planetary motion. The other two laws are more abstract. His second law stated that an imaginary line joining a planet and the sun sweeps out an equal area of space in equal amounts of time. His third law stated that the square of the orbital period of the planets is proportional to the third power of the longest radius of the ellipse. Although having discovered these precise mathematical laws, Kepler could not explain them. They would remain a complete mystery until Newton published his work on gravity.
The same Kepler also conceived of a whole new way to view gravity. While Aristotle had claimed that objects fall because they have the “quality” or “tendency” to move to the center of the universe, Kepler concluded that “it is the earth which attracts the stone, rather than the stone which tends towards the earth.” [293] Revolutionarily, he concluded that all pieces of matter attract each other. He wrote:
If two stones were placed [...] near each other, and beyond the sphere of influence of a third cognate body, these stones, like two magnetic needles, would come together in the intermediate point, each approaching the other by a space proportional to the comparative mass of the other. [294]
In a letter to a patron, he even hypothesized the following:
If we were to place the earth at rest in some place and bring near it a larger earth, the first one would become a weight in relation to the second one and would be attracted by the latter as a stone is attracted by the earth. [293]
Newton’s universal law of gravitation
The British scientist Isaac Newton (1642–1727) managed to create the first accurate theory of gravity, which he described in his Philosophia Naturalis Principia Mathematica (or, in short, the Principia). In this paragraph, I will briefly summarize the brilliant steps he took in order to construct such a theory, for which he is widely considered the greatest genius of all time (rivaled only by Aristotle and Einstein).
Before even considering gravity, Newton first found the correct laws that govern motion itself—his famous three laws of motion. These laws describe with mathematical exactness how objects move with or without the application of external forces. Newton’s first law states that an object in the absence of external forces will stay at rest or continue its motion in a straight line with constant velocity. We already saw this idea in the work of Galileo. In Newton’s words:
Every body perseveres in its state of rest, or of uniform motion in a right line, unless it is compelled to change that state by forces impressed thereon. [295]
Fig. 478 – Isaac Newton by Godfrey Kneller (1689) (University of Cambridge, Britain)
His second law describes how the motion of objects changes when acted upon by an external force. He concluded that force causes a change in momentum (momentum is defined as mass times velocity). In his own words:
The alteration of motion [momentum] is ever proportional to the motive force impressed; and is made in the direction of the right line in which that force is impressed.[21]
His third law states that when object A exerts a force on object B, then object B will simultaneously exert a force on object A of equal magnitude but in the opposite direction. In his own words:
To every Action there is always opposed an equal Reaction: or the mutual actions of two bodies upon each other are always equal, and directed to contrary parts.
Newton then used a thought experiment to show that the same gravitational force that governs the falling of objects on earth can also explain the orbits of the planets. This was in direct contrast to Aristotle’s theory of the universe, who claimed that a different physics was necessary to explain motion on earth and in heaven. Newton envisioned a leaden ball being shot from a large cannon (see Fig. 479). If the cannonball is shot with a small velocity, gravity will quickly curve it downward towards the earth’s surface. However, if the cannonball has exactly the right velocity, the downward curvature of the ball can be made to exactly match the curvature of the earth. If this happens, the ball will continue to fall indefinitely without ever reaching the earth. This, Newton concluded, is how the moon orbits the earth and how the earth and the other planets orbit the sun.
Fig. 479 – Newton’s cannon, from the Principia
Newton then set out to determine a mathematical formula for the magnitude of the gravitational force. He knew that objects near the earth’s surface experience a gravitational acceleration of about 9.8 m/s2 when freely falling. He then calculated the gravitational acceleration with which the moon manages to stay in orbit. To figure this out, he used a formula discovered by the Dutch physicist Christiaan Huygens (1629–1695). Huygens had correctly derived a formula to calculate the acceleration necessary to keep any object in circular motion. Using his formula, he found that the moon accelerates towards the earth with only 0.00273 m/s2. From this, he concluded that at the distance of the moon, the gravitational acceleration has decreased by a factor of about 9.8/0.00273 = 3600. Newton also knew that the distance to the moon was about 60 times the radius of the earth. Since 3600 = 602, he concluded that the gravitational acceleration decreased with the square of the distance. He called this the inverse square law. Using his second and third law of motion, he then found the universal law of gravitation, which in modern language reads:
![]()
But this was just the beginning. In a proof of exceptional genius, Newton showed that only a force that follows his inverse square law caused planets to move in closed elliptical orbits, just as Kepler had observed. Newton then showed that his inverse square law also uniquely satisfied Kepler’s other two laws of planetary motion. Reaching this point, Newton had conclusively shown that the motion of falling objects and the motion of the heavenly orbs could be described by his one universal law of gravitation, thereby unifying terrestrial and celestial physics.
I feign no hypotheses
Newton realized that although his law of gravitation could describe the motion of the planets with astonishing precision, it could not explain how the sun could exert this force on the planets without being in contact with them. Descartes had tried to solve this problem by postulating an undetectable ether that dragged the planets along, but Newton—being a proud follower of Francis Bacon—refused to include such fantasies in his theory. Since there was no evidence for an ether, he decided to leave the question unanswered. When criticized about the absence of a mechanical explanation for gravity, Newton famously added the “General Scholium” to the second edition of the Principia, in which he wrote:
I have not as yet been able to discover the reason for these properties of gravity from phenomena, and I do not feign hypotheses. For whatever is not deduced from the phenomena must be called a hypothesis; and hypotheses, whether metaphysical or physical, or based on occult qualities, or mechanical, have no place in experimental philosophy. In this philosophy, particular propositions are inferred from the phenomena and afterward rendered general by induction. [...] The laws of motion and the law of gravity have been found by this method. And it is enough that gravity really exists and acts according to the laws that we have set forth and is sufficient to explain all the motions of the heavenly bodies and of the sea. [296]
The Age of Newton
Newton’s achievement stunned the intellectual world, leaving the great scientists and philosophers of the 18th century in awe. He had created the first truly successful system of the world, which was mathematically accurate and comprehensive to a degree previously thought impossible. Never before had mankind peered so deeply into the mathematical structure of the universe. Since most thinkers at the time were religious, they believed Newton had found the laws by which God had created the universe.
The great scientist Joseph-Louis Lagrange (1736–1813) supposedly called Newton the greatest genius who has ever lived and also “the most fortunate,” for there could never be another Newton as there was “only one system of the world to discover.” [297] Edmond Halley (1656–1742) concluded:
Nearer the Gods no mortal may approach. [298]
During the 18th and 19th centuries, other scientists picked up where Newton left off, making his legacy even more impressive. Edmond Halley had searched old records of astronomical events and discovered that a certain comet became visible every 75 years. Based on this regularity, he predicted it would return in 1757. Alexis Clairaut (1713–1765) disagreed, concluding that the comet would appear much closer to Jupiter this time, which would slow it down. Based on Newton’s theory, he calculated that it would appear instead in 1758. And so it happened.
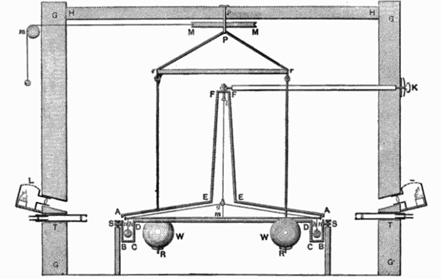
Fig. 480 – Cavendish’s apparatus to determine the mass of the earth
Henry Cavendish (1731–1810) solved a problem that prevented Newton from actually calculating the magnitude of the gravitational force. Newton had shown that the force was proportional to the inverse of the square of the distance, but he did not know how to calculate its exact magnitude. Cavendish solved this problem by directly measuring the gravitational force between four leaden balls in his laboratory (see Fig. 480). Since the gravitational force of the Earth is dependent on its mass, he then used his result to calculate the mass of the entire Earth. He, therefore, called his experiment “weighing the world.”
Pierre-Simon Laplace (1749–1827) and Joseph-Louis Lagrange (1736–1813) were the first to correct a mistake in Newton’s work. Newton had shown that a single planet moving around the sun would move in an elliptical orbit. In reality, however, the different planets also attract each other, causing distortions in their motion. Newton had assumed that these distortions would eventually destabilize the solar system. Since this instability was not observed, Newton assumed that God intervened from time to time to restore the orbits of the planets (in his work Opticks, he wrote that the “mutual actions of comets and planets upon one another” were “apt to increase, till this system wants a reformation” [299]).
Laplace and Lagrange used Newton’s own laws to demonstrate that the largest contributions to these distortions cancel each other out, thereby proving that the solar system will stay intact for an extremely long time. As a result, they saw no need to postulate periodic divine intervention.
Around the end of Laplace’s life, a story began to circulate about a conversation between Laplace and Napoleon. Napoleon asked:
They tell me you have written this large book on the system of the universe, and have never even mentioned its Creator.
Laplace answered:
I had no need of that hypothesis. [300]
Perhaps the greatest triumph of Newton’s theory came in the 19th century when a new planet was discovered based on his laws. Comparing the positions of the planet Uranus in various records, scientists discovered that its orbit changed over time. It was theorized that these changes were caused by the gravitational attraction of a planet yet undiscovered. Urbain Le Verrier (1811–1877) set out to calculate what mass and what position this planet should have to explain the observed deviation. The calculations resulted in specific coordinates, and when a telescope was aimed at exactly this spot, the new planet Neptune was found. It was a sensational moment for science. In the words of a contemporary, Le Verrier had discovered a planet “with the point of his pen.” [301]